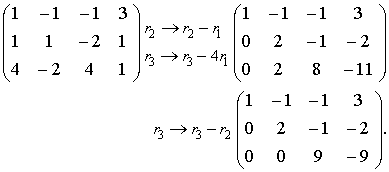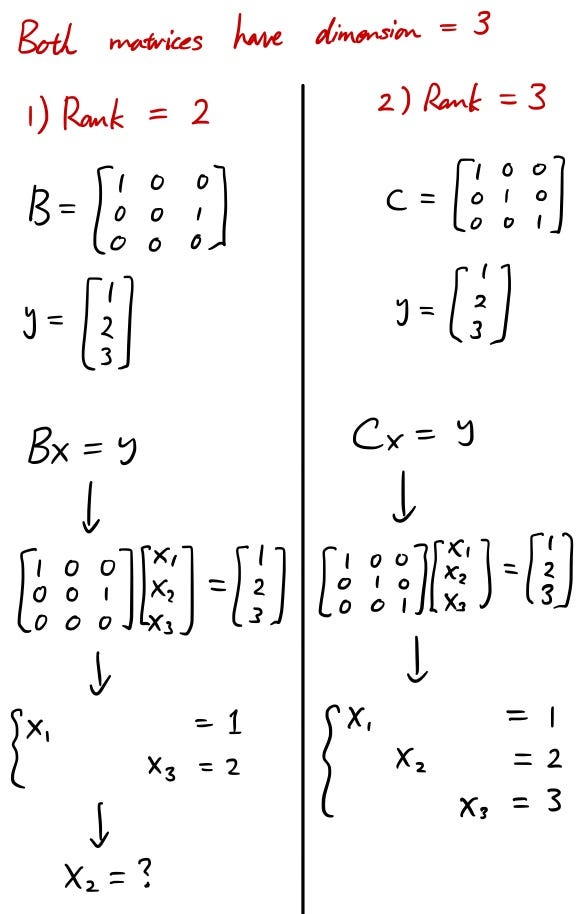Rank Of A Matrix Solved Examples

The rank of a matrix a denoted rank a is the maximum number of independent rows in a.

Rank of a matrix solved examples. Find the rank of the matrix. In this tutorial let us find how to calculate the rank of the matrix. ρ a 3. Let us transform the matrix a to an echelon form.

Testing the consistency of non homogeneous linear equations two and three variables by rank method. Perform the following row operations. It turns out that the rank of a matrix a is also equal to the. This also equals the number of nonrzero rows in r.

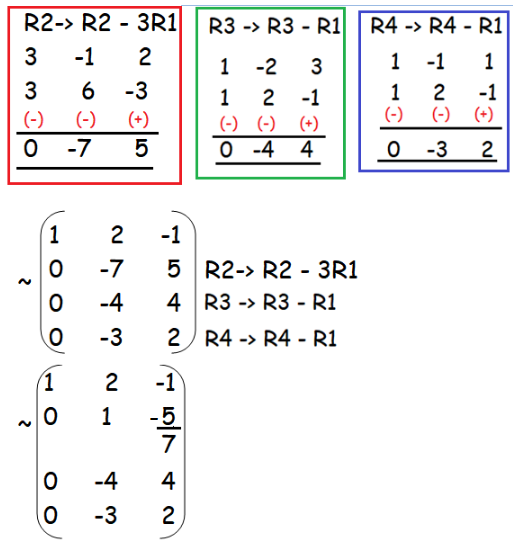
The rank of a matrix which is not in a row echelon form can be found by applying the following result which is stated without proof. Thus the rank of a matrix does not change by the application of any of the elementary row operations. Now two systems of equations are equivalent if they have exactly the same. First because the matrix is 4 x 3 its rank can be no greater than 3.

If a and b are two equivalent matrices we write a b. Find the rank of the matrix a solution. A matrix obtained from a given matrix by applying any of the elementary row operations is said to be equivalent to it. Determine the rank of the 4 by 4 checkerboard matrix.

The rank of a non zero matrix is equal to the number of non zero rows in a row echelon form of the matrix. Find the rank of the matrix by reducing it to a row echelon form. Common math exercises on rank of a matrix. ρ a 3.

The number of non zero rows is 3. 1 2 3 2 4 6 0 0 0 how to calculate the rank of a matrix. Since there are 3 nonzero rows remaining in this echelon form of b example 2. Therefore at least one of the four rows will become a row of zeros.

The order of a is 3 4. For any system with a as a coefficient matrix rank a is the number of leading variables. Note that if a b then ρ a ρ b. Here we view each row in matrix a as a row vector.