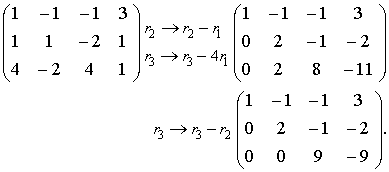Rank Of A Matrix Examples

Note that if a b then ρ a ρ b. A matrix obtained from a given matrix by applying any of the elementary row operations is said to be equivalent to it. The rank of the matrix can be defined in the following two ways.

revlon 1500 tourmaline ceramic replacement brush rocia beige floor decor revitalizing soapstone floors round 6 foot jute rug remove limescale from ceramic tiles research center floor plan architecture royal blue moroccan rug revit heat loss floor

How To Find The Rank Of A Matrix Quora

Mathematics Finding Rank Of Matrix Youtube

Solved 2 Example 8 Provides An Example Of Rank And Nulli Chegg Com

Rank Of A Matrix Solved Example Problems

How To Find Rank Of Matrix Rank Of Matrix Matrices Engineering Mathematics Youtube

Rank Of Matrix

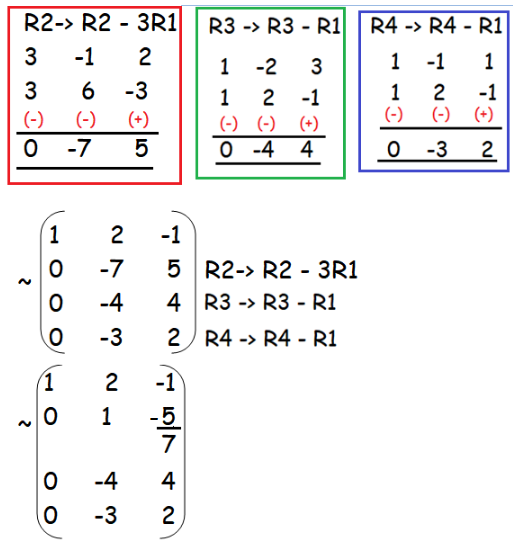
Therefore at least one of the four rows will become a row of zeros.

Rank of a matrix examples. Thus the rank of a matrix does not change by the application of any of the elementary row operations. In this tutorial let us find how to calculate the rank of the matrix. This lesson introduces the concept of matrix rank and explains how the rank of a matrix is revealed by its echelon form. If a and b are two equivalent matrices we write a b.

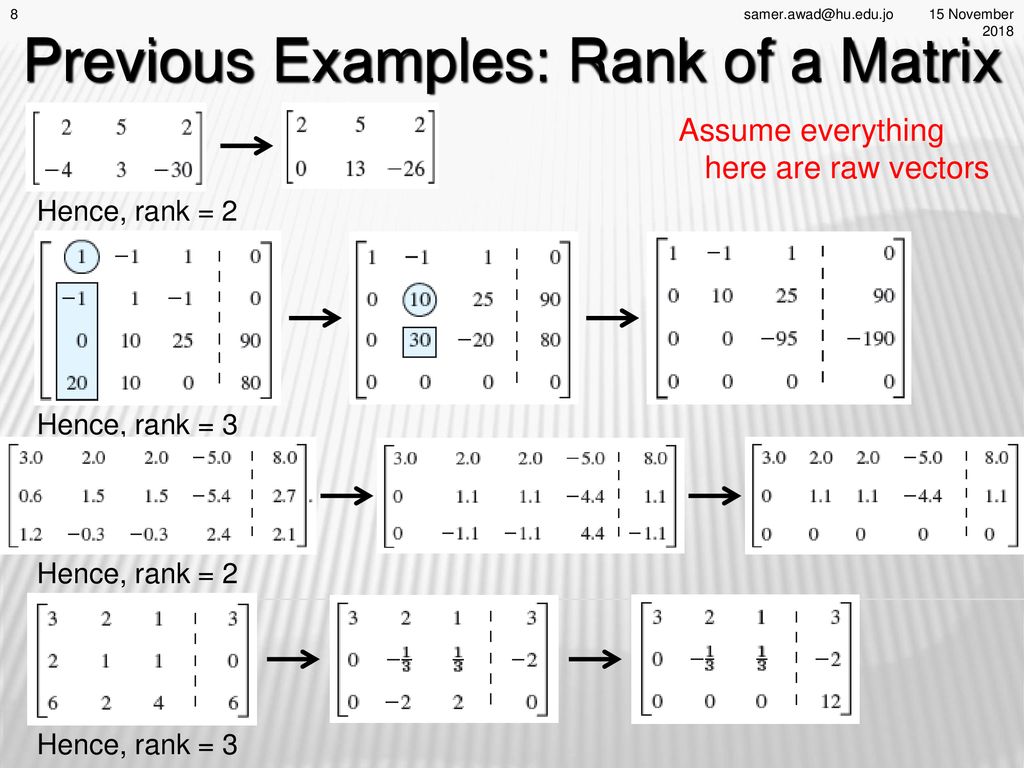
For a 2 4 matrix the rank can t be larger than 2 when the rank equals the smallest dimension it is called full rank a smaller rank is called rank deficient. Perform the following row operations. You can think of an r x c matrix as a set of r row vectors each having c elements. Or rank of the matrix refers to the highest number of linearly independent rows in the matrix.

1 2 3 2 4 6 0 0 0 how to calculate the rank of a matrix. This corresponds to the maximal number of linearly independent columns of this in turn is identical to the dimension of the vector space spanned by its rows. Find the rank of the matrix. The rank of a matrix.

Consider the third order minor 6 0. For example the rank of the below matrix would be 1 as the second row is proportional to the first and the third row does not have a non zero element. First because the matrix is 4 x 3 its rank can be no greater than 3. Consider the third order minor.

In linear algebra the rank of a matrix is the dimension of the vector space generated or spanned by its columns. The rank is at least 1 except for a zero matrix a matrix made of all zeros whose rank is 0. Find the rank of the matrix. Rank of the matrix refers to the highest number of linearly independent columns in a matrix.

Or you can think of it as a set of c column vectors each having r elements. Determine the rank of the 4 by 4 checkerboard matrix. Let a order of a is 3x3 ρ a 3. Introduction to matrix rank.

Let a order of a is 3x3 ρ a 3. There is a minor of order 3 which is not zero ρ a 3. Rank is thus a measure of the nondegenerateness of the system of linear equations and linear transformation encoded by. Find the rank of the matrix.

Your result will be equivalent whether you use the column vectors or the row vectors of the matrix to. Since there are 3 nonzero rows remaining in this echelon form of b example 2.