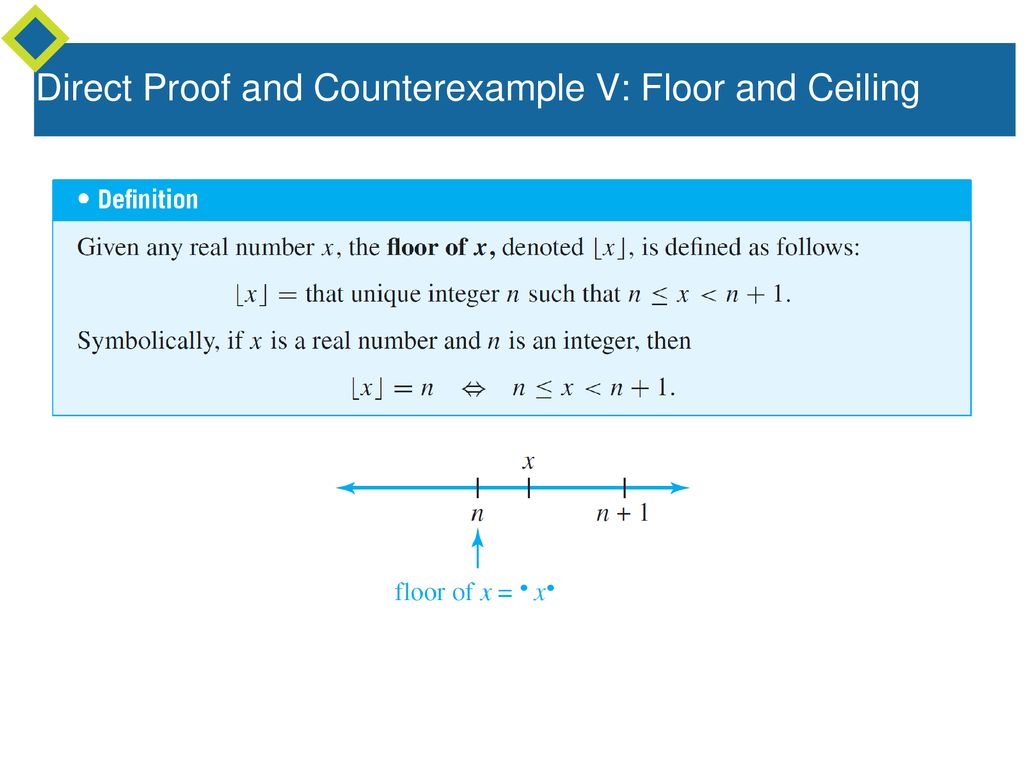
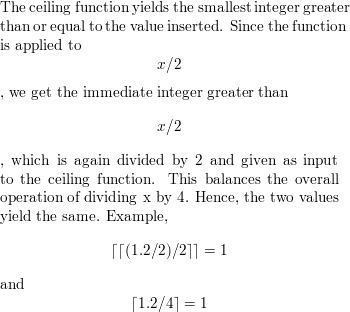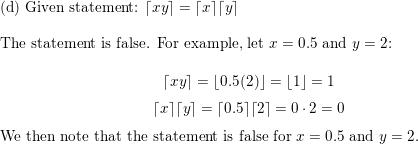Proving Statements About Ceiling And Floor Functions
Https Storm Cis Fordham Edu Zhang Cs2100 Slides Floorceil Pdf
Prove Or Disprove Each Of These Statements About The Floor And Ceiling Functions A X X For All Real Numbers X B X Y X Y For All
Direct Proof And Counterexample V Floor And Ceiling Ppt Download
Proofs Starring Ceiling And Floor Functions Youtube
Example 1 Use Right Angle Congruence Given Ab Bc Dc Bc Prove B C Write A Proof Statement Reasons 1 Given 2 Definitio Proof Writing Writing Theorems
Seven Flipped Youcubed Teachers Math Tasks Math Challenge Mathematical Mindset
Prove or disprove each of these statements about the floor a.
Proving statements about ceiling and floor functions. Certain functions have special properties when used together with floor and ceil. Koether hampden sydney college direct proof floor and ceiling wed feb 13 2013 2 21. We introduce the floor and ceiling functions then do a proof with them. Mathbb r rightarrow mathbb r f.
The remaining statements are shown in a similar manner. Define bxcto be the integer n such that n x n 1. What if we want the floor or ceiling of a number that is already an integer. 1 the floor and ceiling functions 2 theorems 3 applications 4 assignment robb t.
We have solutions for your book. The floor of 2 31 is 2 the ceiling of 2 31 is 3. Floor and ceiling of integers. Like and share the video if it helped.
What is the floor and ceiling of 2 31. R r must be continuous and monotonically increasing and whenever f x f x f x is integer we must have that. In mathematics and computer science the floor function is the function that takes as input a real number and gives as output the greatest integer less than or equal to denoted or similarly the ceiling function maps to the least integer greater than or equal to denoted or. Title definition the floor function let x 2r.
The floor and ceiling functions give us the nearest integer up or down. R r f.
The Floor And Ceiling Functions And Proof Discrete Mathematics Youtube
Example 1 Use Right Angle Congruence Given Ab Bc Dc Bc Prove B C Write A Proof Statement Reasons 1 Given 2 Definitio Proof Writing Writing Theorems
Mrandmrs2015 Home Remodeling Home Kitchen Living
These Rooms Prove That Statement Ceilings Are Taking Over In 2018 Hunker Blue Ceiling Bedroom Bedroom Decor Design Bedroom Makeover
A Beautifully Big And Bright Devol Shaker Kitchen Painted In Damask And Pantry Blue With Brass Details And A Minimalist Dining Room Home Decor Kitchen Interior
Csc 102 Lecture 12 Discrete Structures Previous Lecture Summary Floor And Ceiling Functions Definition Of Proof Methods Of Proof Direct Proof Disproving Ppt Download
Burgin S Ridge Glulam Beams Exposed Duct Work By Form Function Architecture Via Flickr House Ventilation House Interior House
Prove Or Disprove Each Of These Statements About The Floor And Ceiling Functions A X X For All Real Numbers X B 2x 2 X Whenever X Is A Real Number
Surjective Ceiling And Floor Functions Functions And Relations Surjective Functions Youtube
Price Controls Price Floors And Ceilings Illustrated
Price Ceilings Economics
Foundstone Hendrix 1 Light 7 Simple Globe Semi Flush Mount Reviews Wayfair In 2020 Semi Flush Ceiling Lights Flush Ceiling Lights Brass Vanity Light
Multiplication Challenge Multiplication Task Cards Education Elementary Math Task Cards
